第4章線形単回帰モデルの推定と検定

先に出版社サイトよりデータをダウンロードする.

# サポートファイルへのリンク
curl <- "https://www.yuhikaku.co.jp/static_files/05385_support04.zip"
# ダウンロード保存用フォルダが存在しない場合, 作成
if(!dir.exists("downloads")){
    dir.create("downloads")
}
cdestfile <- "downloads/support04.zip"
download.file(curl, cdestfile)
# データ保存用フォルダが存在しない場合, 作成
if(!dir.exists("data")){
    dir.create("data")
}
# WSL上のRで解凍すると文字化けするので、Linuxのコマンドを外部呼び出し
# Windowsの場合は別途コマンドを用いる.
if(.Platform$OS.type == "unix") {
    system(sprintf('unzip -n -Ocp932 %s -d %s', "downloads/support04.zip", "./data"))
} else {
    print("Windowsで解凍するコマンドを別途追加せよ.")
}

必要なライブラリを読み込む.

library(tidyverse)
library(readxl)
library(estimatr)

実証例4.1 労働生産性と実質賃金の関係

p.128の実証例ブロック内の\(N=22\)は\(N=21\)の誤植と思われる.

ch04_wage <- read.csv("data/04_第4章/ch04_wage.csv")
ch04_wage_model <- lm(wage ~ productivity, data = ch04_wage)
summary(ch04_wage_model)
## 
## Call:
## lm(formula = wage ~ productivity, data = ch04_wage)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -47.618 -17.612   4.186  21.946  37.052 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  276.12961   87.61057   3.152  0.00525 ** 
## productivity   0.54682    0.02442  22.395 4.04e-15 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 25.77 on 19 degrees of freedom
## Multiple R-squared:  0.9635, Adjusted R-squared:  0.9616 
## F-statistic: 501.5 on 1 and 19 DF,  p-value: 4.037e-15

Rのlm()で計算される標準誤差は不均一分散に対して頑健でない. 本文中にある不均一分散に対して頑健な計算結果を求めるには, estimatr::lm_robust()を用い, se_type = "stata"と指定する.

ch04_wage_model_robust <- lm_robust(wage ~ productivity, data = ch04_wage, se_type = "stata")
summary(ch04_wage_model_robust)
## 
## Call:
## lm_robust(formula = wage ~ productivity, data = ch04_wage, se_type = "stata")
## 
## Standard error type:  HC1 
## 
## Coefficients:
##              Estimate Std. Error t value  Pr(>|t|) CI Lower CI Upper DF
## (Intercept)  276.1296   71.25559   3.875 1.019e-03  126.990 425.2693 19
## productivity   0.5468    0.02046  26.722 1.553e-16    0.504   0.5896 19
## 
## Multiple R-squared:  0.9635 ,    Adjusted R-squared:  0.9616 
## F-statistic: 714.1 on 1 and 19 DF,  p-value: < 2.2e-16

図4-1 時間当たり実質賃金と労働生産性

回帰曲線はgeom_smooth()で描画できる.

ch04_wage %>%
    ggplot(aes(x = productivity, y = wage)) +
    geom_point() +
    xlab("労働生産性 (円)") +
    ylab("実質賃金 (円)") +
    geom_smooth(method = "lm", se = FALSE, color = "black")
## `geom_smooth()` using formula = 'y ~ x'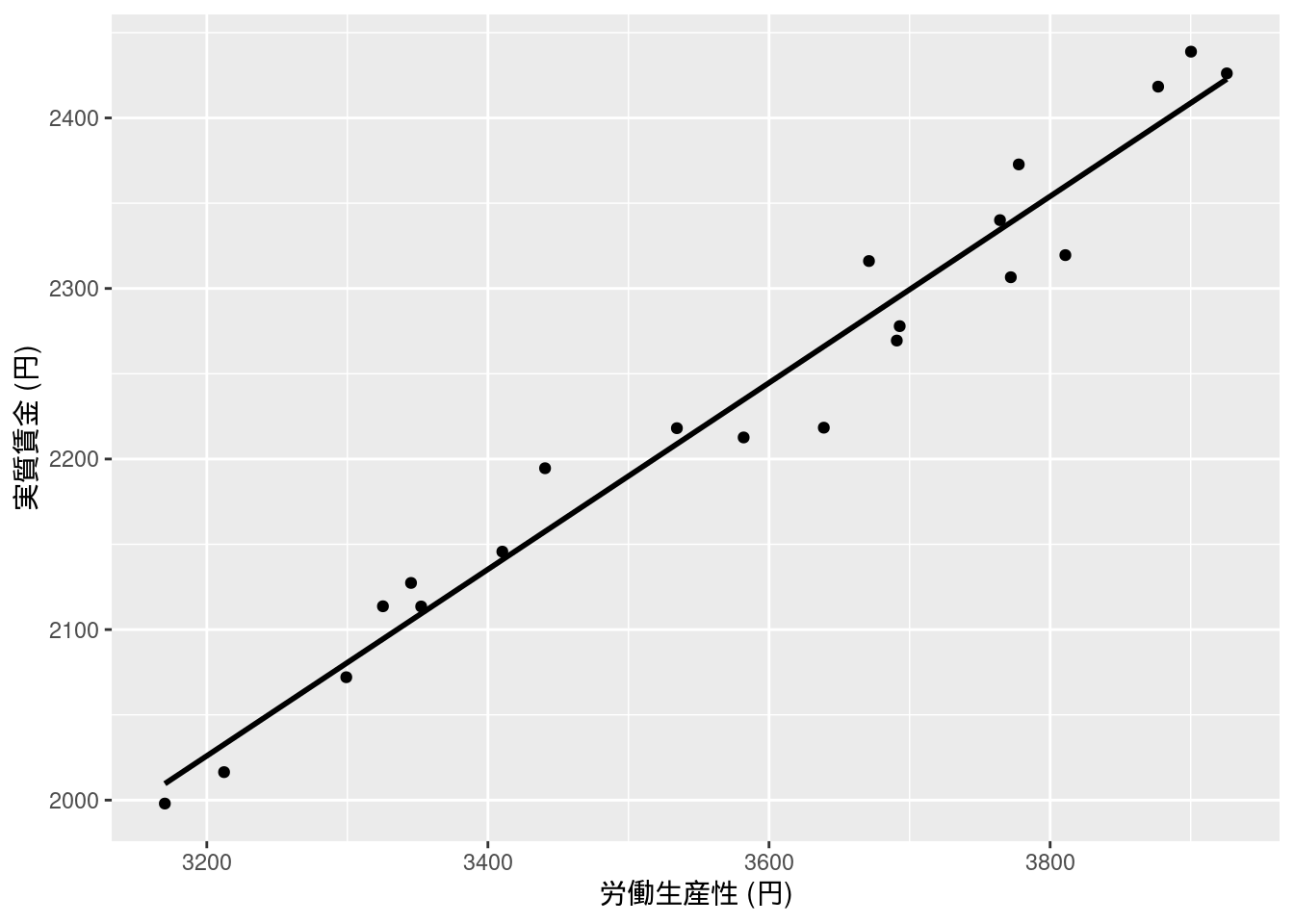

練習問題 4-2 [実証]

データを読み込み, 回帰分析を実行する. Excelファイルの読み込みにはreadxl::read_excel()を用いる. このパッケージはtidyverseに付帯しているが, 別途読み込む必要がある. 列名が日本語だと扱いづらいため, これを変更しておく. \(gdp2013\_ln = \beta_0 + \beta_1 pop2013\_ln\)というモデルを立てると, \(\hat{\beta_0} = 7.623, \hat{\beta_1} = 1.075\)と求められる.

data42 <- read_excel("data/04_第4章/data for chap 4 exercise 2.xlsx")
colnames(data42) <- c("pref", "pop2013", "gdp2013", "pop2013_ln", "gdp2013_ln")

model42 <- lm(gdp2013_ln ~ pop2013_ln, data = data42)
model42
## 
## Call:
## lm(formula = gdp2013_ln ~ pop2013_ln, data = data42)
## 
## Coefficients:
## (Intercept)   pop2013_ln  
##       7.623        1.075

帰無仮説\(H_0\): \(\beta_1 = 1\)に関して, 統計量\(t = \frac{\hat{\beta_1} - \beta_1}{\text{SE}(\hat{\beta_1})} = 2.62773\)が求められる. これは自由度\(n-2 = 45\)で, 有意水準5%のt検定の棄却域\((\infty, -2.014103]\), \([2.014103, \infty)\)に入っていることから帰無仮説は棄却される.

beta1 <- model42$coefficients[2]
sebeta1 <- summary(model42)$coefficients[2, 2]
n <- dim(data42)[1]

t <- (beta1 - 1)/sebeta1
t
## pop2013_ln 
##    2.62773
qt(0.975, n-2) # 2.014103
## [1] 2.014103

confint()関数を用いると直接求められる.

confint(model42, '(Intercept)', level=0.90)
##                  5 %     95 %
## (Intercept) 7.257252 7.988132

人口が1%変化すると, GDPは\(\beta_1 = 1.075\)%変化する.
\(\text{Var}(u) = \frac{\sum_{i=1}^n \hat{u}_i^2}{n-2} = 0.02245859\)と求められる. ln(人口)の分散はvar()関数を用いると, 0.5964525と求められる.

sum(model42$residuals^2)/(n-2)
## [1] 0.02245859

var_pop2013_ln <- var(data42$pop2013_ln)
var_pop2013_ln
## [1] 0.5964525

練習問題 4-10 [実証]

データを読み込み, 回帰分析を実行することで\(\beta_1\)を一致推定できるか調べる. 実際に計算すると, Cov\((u_i, X_i) = 0\)が成り立っていることが確認できる.

data410 <- read_excel("data/04_第4章/data for chap 4 exercise 10.xlsx") %>% data.frame()
model410 <- lm(Y ~ X, data = data410)
cov(model410$residuals, data410$X)
## [1] 3.643979e-17

E\((u_i^2|X_i) = 0.690318 \neq 0\). 散布図を描くと, \(\hat{Y}_i\)が大きくなるに従って残差の分散が大きくなっていることが確認できる.

mean(model410$residuals^2)
## [1] 0.690318

model410 %>%
    ggplot(aes(x = .fitted, y = .resid)) +
    geom_point() +
    geom_hline(yintercept = 0)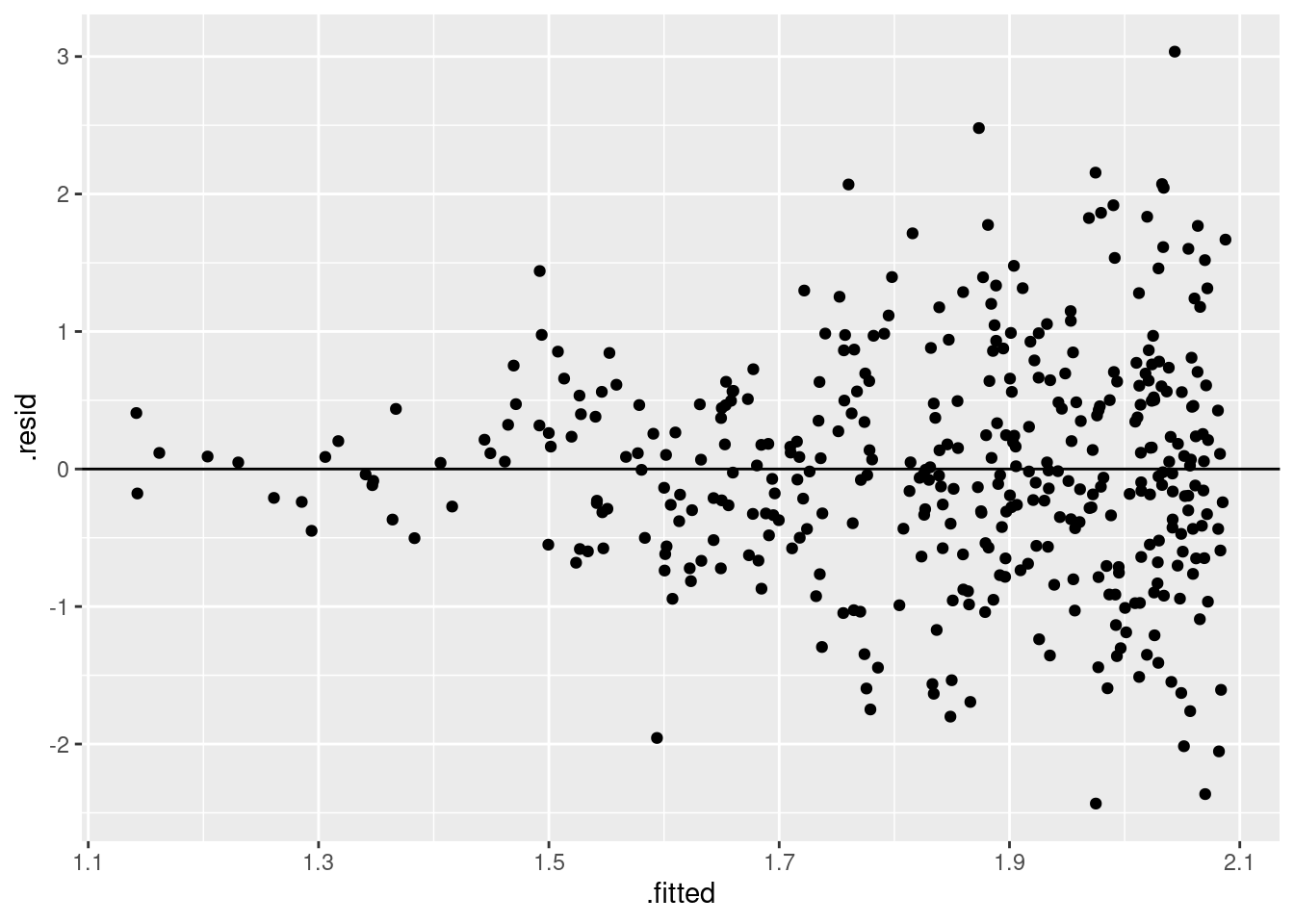

不均一分散に頑健な標準誤差はestimatr::lm_robust()を用いて求める.

model410_robust <- lm_robust(Y ~ X, data = data410)
summary(model410_robust)
## 
## Call:
## lm_robust(formula = Y ~ X, data = data410)
## 
## Standard error type:  HC2 
## 
## Coefficients:
##             Estimate Std. Error t value  Pr(>|t|) CI Lower CI Upper  DF
## (Intercept)   0.8103     0.1583   5.119 4.803e-07   0.4991    1.122 398
## X             1.2773     0.2158   5.918 7.035e-09   0.8530    1.702 398
## 
## Multiple R-squared:  0.05683 ,   Adjusted R-squared:  0.05446 
## F-statistic: 35.02 on 1 and 398 DF,  p-value: 7.035e-09

summary()によると, \(\beta_1\)の95%信頼区間に0.8は入っていないため, 帰無仮説は棄却されない.

不均一分散に頑健な標準誤差はestimatr::lm_robust()を用いて求める.

confint(model410)
##                 2.5 %   97.5 %
## (Intercept) 0.3912772 1.229412
## X           0.7645056 1.790022

summary()によると, \(\beta_1\)の95%信頼区間に0.8は入っており, 帰無仮説は棄却される.

分散が均一でないデータに均一分散を仮定した標準誤差を用いると, 上のように異なる結果が導かれることがある.

第4章 線形単回帰モデルの推定と検定

実証例4.1 労働生産性と実質賃金の関係

図4-1 時間当たり実質賃金と労働生産性

練習問題 4-2 [実証]

練習問題 4-10 [実証]

第4章線形単回帰モデルの推定と検定